Solving an advanced math problem independently requires the coordination of a number of complex skills. The student must have the capacity to reliably implement the specific steps of a particular problem-solving process, or cognitive strategy. At least as important, though, is that the student must also possess the necessary metacognitive skills to analyze the problem, select an appropriate strategy to solve that problem from an array of possible alternatives, and monitor the problem-solving process to ensure that it is carried out correctly.
The following strategies combine both cognitive and metacognitive elements (Montague, 1992; Montague & Dietz, 2009). First, the student is taught a 7-step process for attacking a math word problem (cognitive strategy). Second, the instructor trains the student to use a three-part self-coaching routine for each of the seven problem-solving steps (metacognitive strategy).
In the cognitive part of this multi-strategy intervention, the student learns an explicit series of steps to analyze and solve a math problem. Those steps include:
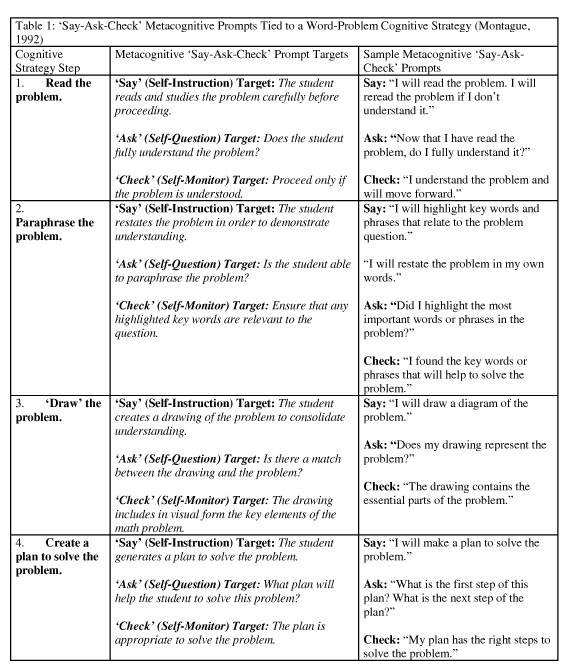
1. Reading the problem. The student reads the problem carefully, noting and attempting to clear up any areas of uncertainly or confusion (e.g., unknown vocabulary terms).
2. Paraphrasing the problem. The student restates the problem in his or her own words.
3. ‘Drawing’ the problem. The student creates a drawing of the problem, creating a visual representation of the word problem.
4. Creating a plan to solve the problem. The student decides on the best way to solve the problem and develops a plan to do so.
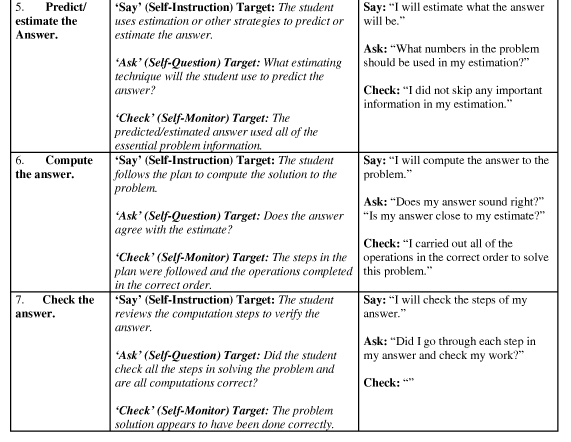
5. Predicting/Estimating the answer. The student estimates or predicts what the answer to the problem will be. The student may compute a quick approximation of the answer, using rounding or other shortcuts.
6. Computing the answer. The student follows the plan developed earlier to compute the answer to the problem.
7. Checking the answer. The student methodically checks the calculations for each step of the problem. The student also compares the actual answer to the estimated answer calculated in a previous step to ensure that there is general agreement between the two values.
The metacognitive component of the intervention is a three-part routine that follows a sequence of ‘Say’, ‘Ask, ‘Check’. For each of the 7 problem-solving steps reviewed above:
- The student first self-instructs by stating, or ‘saying’, the purpose of the step (‘Say’).
- The student next self-questions by ‘asking’ what he or she intends to do to complete the step (‘Ask’).
- The student concludes the step by self-monitoring, or ‘checking’, the successful completion of the step (‘Check’).
While the Say-Ask-Check sequence is repeated across all 7 problem-solving steps, the actual content of the student self-coaching comments changes across the steps.
Table 1 shows how each of the steps in the word problem cognitive strategy is matched to the three-part Say-Ask-Check sequence:
Students will benefit from close teacher support when learning to combine the 7-step cognitive strategy to attack math word problems with the iterative 3-step metacognitive Say-Ask-Check sequence. Teachers can increase the likelihood that the student will successfully acquire these skills by using research-supported instructional practices (Burns, VanDerHeyden, & Boice, 2008), including:
- Verifying that the student has the necessary foundation skills to solve math word problems
- Using explicit instruction techniques to teach the cognitive and metacognitive strategies
- Ensuring that all instructional tasks allow the student to experience an adequate rate of success
- Providing regular opportunities for the student to be engaged in active accurate academic responding
- Offering frequent performance feedback to motivate the student and shape his or her learning.
References
Thomas & J. Grimes (Eds.), Best practices in school psychology V (pp.1151-1162). Bethesda, MD: National Association of School Psychologists.
Montague, M. (1992). The effects of cognitive and metacognitive strategy instruction on the mathematical problem solving of middle school students with learning disabilities. Journal of Learning Disabilities, 25, 230-248.
Montague, M., & Dietz, S. (2009). Evaluating the evidence base for cognitive strategy instruction and mathematical problem solving. Exceptional Children, 75, 285-302.
Reprinted with permission from Jim Wright from www.interventioncentral.org.
Download Information
To view or print this handout you have the following options:
View or Download PDF Version of “Math Problem-Solving: Combining Cognitive & Metacognitive Strategies in a 7-Step Process” – PDF (Right Click and Choose Save)
View or Download MS Word Version of- “Math Problem-Solving: Combining Cognitive & Metacognitive Strategies in a 7-Step Process” – Word Doc (Right Click and Choose Save)

